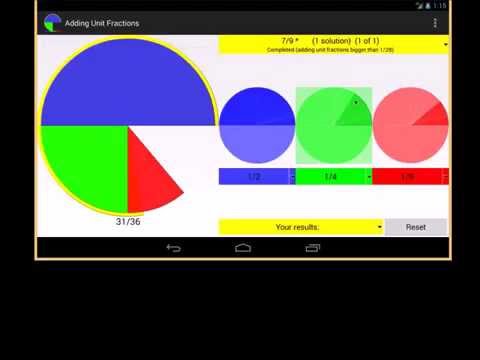
Adding unit fractions

Name: Adding unit fractions
Availability: InStock
Author: nummolt

nummolt

10 мың+

Жүктеп алынғандар

Барлығы үшін

Осы қолданба туралы

Қосымшада 21 қиындықты жеңу ұсынылған.
Қосымшаның жоғарғы жағында көрсетілген тиісті фракцияларды алу, екі немесе үш бөлік фракциясын қосу.

Ұсынылған тиісті бөлшектердің әр түрлі шешімдері болады.
Әр түрлі деңгейдегі қиындықтар

Бірдей фракцияны бірдей мәнмен қайталай алмайсыз.
Бағдарламада сіз ағымдағы проблемада табылған барлық шешімдерді жою және нөлден бастайтын батырманы таба аласыз.
Бұл қосымшада қолданылатын littlest бөлігінің үлесі 1/28 құрайды.

Бағдарлама осындай есептерді шешуде фракцияларды бөлудің пайдалы жақтарын көрсетуге арналған.

Www.nummolt.com сайтынан
Бұл www.mathcats.com сайтымен бірлесіп жасалған «Ежелгі Египеттің фракциялары» эволюциясы

Кеңес:
Біздің дәуірімізге дейінгі 1650 жылы Ринд математикалық папирусында (RMP) хатшы Ахмес патша Аменемамхат III патшалығынан жоғалған тестті көшірді.
Папирустың бірінші бөлігін кесте 2 / n алады. 3-тен 101-ге дейінгі тақ сан үшін 2 / n фракциясы бірлік фракциялардың қосындысы түрінде өрнектеледі.
Бұл қосымшада сіз Ахмес декомпозицияларының бірнешеуін (2/3, 2/5, 2/7, 2/9), сонымен бірге ол тастаған элементтерді жасай аласыз.
Бағдарлама сонымен қатар ыдырауға мүмкіндік береді: 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10.
Қалған мәселелерді шешу үшін сіз 2 / n ыдырауды шеше отырып алған білімді пайдалана аласыз.
Толығырақ: http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html

«Дұрыс фракциялар» қосымшасы (сол әзірлеуші) - «бөлшек бөлшектерін қосу» мәселесін шешуге көмектесетін дұрыс құрал.

Осы қосымшаның Merlot сілтемесі:
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
Курстар:
Математика 1, 2 және 3: Бөлшектер
Математика 4: Жазу фракциялары, Эквивалентті фракциялар, Салыстыру және ретке келтіру, Бөлшектерді жеңілдету, Бөлшектерді қосу, Бөлшектерді азайту
Математика 5, 6 және 7: Жазу фракциялары, Эквивалентті фракциялар, Салыстыру және ретке келтіру, Бөлшектерді жеңілдету, Бөлшектерді қосу, Бөлшектерді азайту, Көбейту, Бөлшектерді бөлу

Кімнен: nummolt.com
Nummolt қолданбалары:
«Математика - бұл ең қиын ойыншық. Бала қаншалықты қиын болса да, оларды ешқашан сындыра алмайды»

Жаңартылған күні

2023 ж. 16 қар.

Дерек қауіпсіздігі

Қауіпсіздік ұғымы әзірлеушілердің деректеріңізді қалай жинап, бөлісетінін түсінуден басталады. Дерек құпиялығы мен қауіпсіздік шаралары қолданбаңыздың пайдаланылуына, аймағыңыз бен жасыңызға байланысты әртүрлі болуы мүмкін. Бұл ақпаратты әзірлеуші ұсынды және оны өзгертіп тұруы мүмкін.