Adding unit fractions
10 tūkst.+
Lejupielādes
Visiem
info
Par šo lietotni
Lietotne piedāvā 21 izaicinājumu, kas jāpārvar.
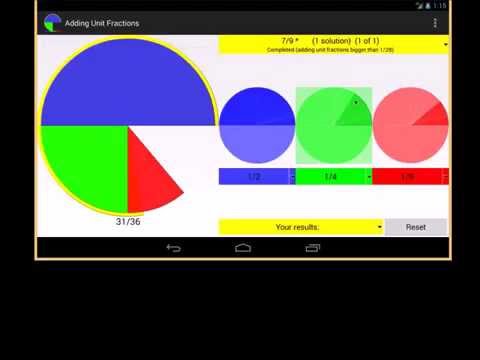
Pareizu frakciju iegūšana, kas uzskaitītas lietojumprogrammas augšdaļā, pievienojot divu vai trīs vienību frakcijas.
Katrā piedāvātajā pareizā frakcijā ir mainīgs risinājumu skaits.
Un dažādi grūtības līmeņi
Jūs nevarat atkārtot vienības frakcijas ar tādu pašu vērtību.
Lietotnē atradīsit pogu, lai izdzēstu visus pašreizējās problēmas risinājumus un sāktu no jauna.
Šajā lietotnē mazākā vienības daļa ir 1/28.
Programma ir izstrādāta, lai parādītu frakciju atņemšanas lietderību šādu problēmu risināšanā.
No vietnes www.nummolt.com
Šī ir "Vecās Ēģiptes frakciju" evolūcija, kas tapusi sadarbībā ar www.mathcats.com
Padoms:
Rhind Mathematical Papyrus (RMP) 1650. gadā pirms mūsu ēras rakstu mācītājs Ahmess nokopēja tagad zaudēto pārbaudījumu no karaļa Amenemamata III valdīšanas.
Pirmo papirusa daļu aizņem tabula 2 / n. Frakcijas 2 / n nepāra n diapazonā no 3 līdz 101 izsaka kā vienības frakciju summas.
Šajā lietotnē jūs varat izveidot dažus no Ahmes sadalījumiem (2/3, 2/5, 2/7, 2/9) un arī viņa iznīcinātos.
Lietotne ļauj sadalīties arī: 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10.
Jūs varat izmantot iegūtās zināšanas, risinot 2 / n sadalījumus, lai atrisinātu pārējās problēmas.
Vairāk: http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html
Lietotne “Pareiza frakcija” (tas pats izstrādātājs) ir pareizais rīks, kas palīdz atrisināt “vienības frakciju pievienošanu”.
Šīs lietotnes Merlot atsauce:
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
Kursi:
1., 2. un 3. matemātika: frakcijas
Matemātika 4: Frakciju rakstīšana, Ekvivalentās frakcijas, Salīdzināšana un pasūtīšana, Frakciju vienkāršošana, Frakciju pievienošana, Frakciju atņemšana
5., 6. un 7. matemātika: Frakciju rakstīšana, Ekvivalentās frakcijas, Salīdzināšana un pasūtīšana, Frakciju vienkāršošana, Frakciju pievienošana, Frakciju atņemšana, Frakciju reizināšana, Frakciju dalīšana
No: nummolt.com
Nummolt lietotnes:
"Matemātika ir visstingrākā rotaļlieta. Lai cik bērns būtu nožēlojams, viņš nekad to nespēs salauzt."
Pareizu frakciju iegūšana, kas uzskaitītas lietojumprogrammas augšdaļā, pievienojot divu vai trīs vienību frakcijas.
Katrā piedāvātajā pareizā frakcijā ir mainīgs risinājumu skaits.
Un dažādi grūtības līmeņi
Jūs nevarat atkārtot vienības frakcijas ar tādu pašu vērtību.
Lietotnē atradīsit pogu, lai izdzēstu visus pašreizējās problēmas risinājumus un sāktu no jauna.
Šajā lietotnē mazākā vienības daļa ir 1/28.
Programma ir izstrādāta, lai parādītu frakciju atņemšanas lietderību šādu problēmu risināšanā.
No vietnes www.nummolt.com
Šī ir "Vecās Ēģiptes frakciju" evolūcija, kas tapusi sadarbībā ar www.mathcats.com
Padoms:
Rhind Mathematical Papyrus (RMP) 1650. gadā pirms mūsu ēras rakstu mācītājs Ahmess nokopēja tagad zaudēto pārbaudījumu no karaļa Amenemamata III valdīšanas.
Pirmo papirusa daļu aizņem tabula 2 / n. Frakcijas 2 / n nepāra n diapazonā no 3 līdz 101 izsaka kā vienības frakciju summas.
Šajā lietotnē jūs varat izveidot dažus no Ahmes sadalījumiem (2/3, 2/5, 2/7, 2/9) un arī viņa iznīcinātos.
Lietotne ļauj sadalīties arī: 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10.
Jūs varat izmantot iegūtās zināšanas, risinot 2 / n sadalījumus, lai atrisinātu pārējās problēmas.
Vairāk: http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html
Lietotne “Pareiza frakcija” (tas pats izstrādātājs) ir pareizais rīks, kas palīdz atrisināt “vienības frakciju pievienošanu”.
Šīs lietotnes Merlot atsauce:
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
Kursi:
1., 2. un 3. matemātika: frakcijas
Matemātika 4: Frakciju rakstīšana, Ekvivalentās frakcijas, Salīdzināšana un pasūtīšana, Frakciju vienkāršošana, Frakciju pievienošana, Frakciju atņemšana
5., 6. un 7. matemātika: Frakciju rakstīšana, Ekvivalentās frakcijas, Salīdzināšana un pasūtīšana, Frakciju vienkāršošana, Frakciju pievienošana, Frakciju atņemšana, Frakciju reizināšana, Frakciju dalīšana
No: nummolt.com
Nummolt lietotnes:
"Matemātika ir visstingrākā rotaļlieta. Lai cik bērns būtu nožēlojams, viņš nekad to nespēs salauzt."
Atjaunināta
Drošība sākas ar izpratni par to, kā izstrādātāji vāc un kopīgo jūsu datus. Datu konfidencialitātes un drošības prakse var atšķirties atkarībā no izmantojuma, reģiona un vecuma. Izstrādātājs ir sniedzis šo informāciju un laika gaitā var to atjaunināt.
Dati netiek kopīgoti ar trešajām pusēm
Uzziniet vairāk par to, kā izstrādātāji norāda datu kopīgošanu.
Dati netiek vākti
Uzziniet vairāk par to, kā izstrādātāji norāda datu vākšanu.
Apņemšanās ievērot Play ģimenes satura politiku
Jaunumi
name 1.1.6 v.12 Update to Android 13 sdk34 + Privacy Policy
Lietotnes atbalsts
phone
Tālruņa numurs
+34600336495
Par izstrādātāju
Maurici Carbó Jordi
double.struck.capital@gmail.com
C. SAN ANTONI MARIA CLARET 324 46
08041 Barcelona
Spain