Number Series Calculator

PLATANUS

Contains ads

About this app

The purpose of Number Series Calculator is to help everyone learn how to solve problems with number series that are used in various tests and exams such as IQ Tests, Math Exams or Job Aptitude Tests. This application can be useful to all math lovers.

This application is free and does not require an internet connection.

This version of the application contains ads.
You can download the paid version without ads.
Visit Number Series Calculator Next

With Number Series Calculator you can
- find the next or missing terms in a number series
- find the formula (pattern) of an arithmetic sequence
- see a sequence graph or a graph of your own math function

This app not only calculates the missing numbers and letters of the sequence, but also finds the formula and in some cases, the name of the sequence (Fibonacci Series, Arithmetic Progression, Geometric Progression, Prime Numbers etc) . You can also see a graphical representation of the sequence or your own function.

With Number Series Calculator you can also
- calculate Sum of the N Terms of the sequence
- analyze many different types of number series ( Fibonacci series , Arithmetic Sequence, Geometric Sequence etc. )
- calculate partial sums (a Partial Sum is the sum of part of the sequence)
- use simple math expressions. For example you can input 1/2, 2/3, ?/4, 4/?, 5/6 or (1+2)/1, (1+3)/2, (1+4)/3, ?.
- calculate the value of the custom formula
- copy and send results to other applications

Symbol ^ used to represent exponentiation. For example, 2^2 means 4 .

You can use this application to calculate your own expression (javascript syntax).
For example, to calculate square numbers create custom formula and set expression to 'n * n'. If you want calculate sin or cos, create custom formula and set expression to Math.sin(n) or Math.cos(n). You can use any javascript function.
You can calculate any recursive formula, for example, 'a[n-1] + a[n-2]' .

Number Series Calculator can use custom formulas to calculate the next and missing numbers in the number sequences.

In addition to the next and missing items of the sequence, the application determines its type and formula (pattern).

To solve problems with letter sequences, you need to select your alphabet in the settings.
If your alphabet is not in the list, select 'Other' and enter all the letters of your
alphabets separated by a comma in the field that follows the list of alphabets.
Example a, b, c, d, e, f, g.

This app may also be helpful in preparing for the next tests:
- online assessment test for jobs
- employment assessment test
- pre employment assessment test
- pre employment screening tests
- employment aptitude test
- skills assessment test for employment
- number series reasoning test

Examples ( from IQ Test )

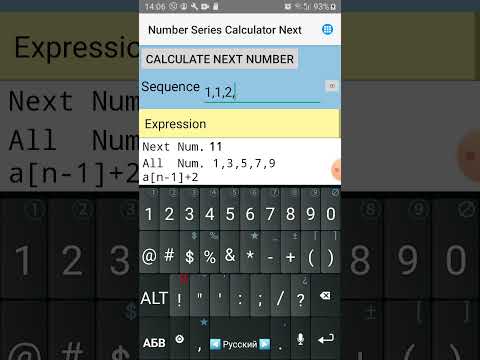
1. What number comes next in the arithmetic sequence ?
1,1,2,3,5,8,13
Result:
Next Number = 21
Sequence Name: Fibonacci Sequence

2. What number comes next in the math sequence ?
1,3,5,7,9,11,13,15
Result:
Next Number = 17
Sequence Name: Arithmetic Progression

3. What number comes next in the numeric sequence ?
1,2,4,8,16,32
Result:
Next Number = 64
Sequence Name: Geometric Progression

For best results, please, run application 2-3 times.

Ratings and reviews

You need to use , between numbers, I don't think a lot of people understand this. So maybe a little ? Icon that people can click to read how it works. Besides that it works perfectly, I like doing these riddles but if you get them wrong they don't always explain why. This app helps you figure out what they wanted.

Maybe it can be improvable, but it is an awesome idea. It can help in dramatic ways many activities. Thank you

Please add : Copy paste button Clear all button Edit : yes. I mean copy paste results and clear sequence buttons. Thank you

What's new

If no solution is found, the program will not show ads in an empty list.