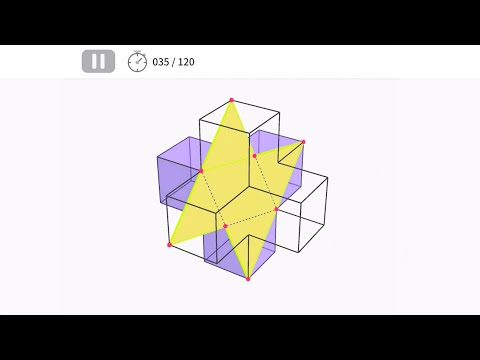
究極の立体＜切断＞

hanamarugroup

Sobre l'aplicació

● El primer d'una sèrie de preparacions definitives per a les proves d'accés a l'escola secundària creades per un equip de desenvolupadors d'aplicacions educatives amb 1 milió d'usuaris!
● S'han analitzat 10 anys de preguntes anteriors d'escoles famoses i s'han seleccionat acuradament 100 preguntes!
● Dominar el camp que apareix amb freqüència de les proves d'accés a l'escola secundària, el ``tall tridimensional''!

◆ Quin tipus de material didàctic és el millor tridimensional?

Es tracta d'una aplicació de material didàctic que conté 100 problemes sobre el ``tall 3D'', un camp que apareix amb freqüència a les matemàtiques de l'examen d'accés a secundària, i us permet girar i tallar lliurement els objectes 3D reproduïts mentre apreneu.
En condensar els coneixements sobre els materials didàctics d'aplicació de Hanamaru Lab, que desenvolupa l'aplicació de desenvolupament de la capacitat de pensament ``Think Think'' amb 1 milió d'usuaris, i el coneixement de l'orientació dels exàmens d'accés a l'escola secundària de la famosa escola cram ``Hanamaru Gakushukai'', hem desenvolupat un mètode de tall tridimensional. Cultiva la capacitat d'"imaginar la manera com mires un problema".
Aquest llibre conté 100 preguntes que cobreixen tots els patrons, basades en una anàlisi de preguntes tridimensionals reals que es van fer als exàmens d'accés a matemàtiques de secundària durant els darrers 10 anys.


◆Per què és important el tall en 3D?
- Camps que apareixen amb freqüència a les proves d'accés a secundària. El dibuix de la secció transversal precisa és essencial!
El tall tridimensional és una àrea important i freqüent en matemàtiques per als exàmens d'accés a secundària. Les preguntes es fan sovint com a preguntes grans i, si no pots dibuixar el pla de tall amb precisió, hi ha molts casos en què fallaràs totes les preguntes. Ser capaç d'imaginar i dibuixar amb precisió un diagrama de secció transversal és un requisit previ important per abordar un problema.

- És difícil aprendre a la pissarra o al paper!
S'ha dit que el tall tridimensional és difícil de tractar perquè requereix una consciència espacial avançada i una capacitat de manipulació d'imatges. Per molt que estudiïs en una superfície plana com una pissarra o un paper, encara que creguis que ho entens en aquell moment, hi ha molts casos en què si l'angle canvia una mica o el punt de tall canvia, no ho entendràs. en absolut. Moltes famílies han provat de tallar verdures i esponges a casa per assaig i error, però aquest mètode era difícil de reproduir formes complexes i tallar superfícies, i no era adequat per a l'aprenentatge repetit.

- Si ho domines, serà un gran avantatge!
Tot i ser un camp important, molts estudiants lluiten amb ell, però si el domines, tindreu un gran avantatge. ``Ultimate 3D Cutting'' aconsegueix els tres punts següents: 1) moure i tallar l'objecte 3D tu mateix, 2) estudiar amb cura les preguntes més freqüents de l'examen d'accés a secundària seleccionades i 3) estudiar repetidament els tres principis. Aquest és l'únic aplicació que us permet especialitzar-vos en tall 3D amb un enfocament completament diferent de l'aprenentatge anterior.



◆Tres principis de tall tridimensional

1. "Mateix pla": "Si hi ha dos punts en el mateix pla, el tall sempre passarà per la recta que uneix els dos punts. Per tant, es poden connectar punts del mateix pla.

2. "Paral·lel": Si les superfícies són paral·leles, les línies de tall de cada superfície seran sempre paral·leles. Per tant, si ja s'ha traçat una recta al pla B que és paral·lela al pla A, podeu dibuixar una recta al pla A que passi pel punt i sigui paral·lela a la recta del pla B.

3. "Ampliar": en estendre la línia de tall i els costats del sòlid, podeu trobar un punt fora del sòlid on el tall passa per la intersecció. Podeu dibuixar una línia des del punt trobat fent servir 1. ``coplanar'' i 2. ``paral·lel''.


◆Propòsit d'aquest material didàctic
Les matemàtiques de l'examen d'accés a l'escola secundària japonesa estan plenes de preguntes interessants i meravelloses que posen a prova les vostres habilitats de pensament i imaginació.
Creiem que l'acte d'afrontar i resoldre aquests problemes hauria de ser una experiència intel·lectualment emocionant i emocionant.
D'altra banda, és cert que a causa de l'alt nivell de pensament i habilitats d'imaginació requerides, els resultats de l'aprenentatge tradicional en paper o pissarra es tendeixen a atribuir al "sentit innat".
Esperem que les matemàtiques per als exàmens d'accés a secundària es converteixin en una experiència d'aprenentatge intel·lectualment dinàmica a la qual tothom pugui participar amb il·lusió. Començarem centrant-nos en el "tall tridimensional", que és una assignatura que es troba amb freqüència i que molts els nens tenen dificultats. Jo n'he fet un tema.
Com que és una aplicació, podeu reproduir l'objecte 3D com si el tinguéssiu a la mà. A mesura que us divertiu aprenent mentre gireu i talleu sòlids perfectament reproduïts, podreu visualitzar qualsevol superfície de tall, reproduir, girar i tallar el sòlid del vostre cap sense dependre de la tècnica o la memorització.
Creiem que poder convertir un punt feble en un fort donarà als nens una sòlida sensació de confiança, i que les habilitats de consciència espacial que desenvolupen es convertiran en un gran actiu, més enllà d'estudiar, fins i tot després de fer la prova d'accés.

◆Com utilitzar
・Seleccioneu el problema que voleu reproduir a la pantalla de selecció del problema.
- Si premeu cadascun dels tres botons (3 principis de tall en 3D) a la part inferior dreta de la pantalla de reproducció i toqueu la superfície que voleu dibuixar una línia, només podeu dibuixar una línia si la resposta és correcta.
- Un cop hagis dibuixat totes les línies que conformen el tall, es mostraran els resultats de la jugada.
・ Cada vegada que acabis de resoldre una pregunta, podràs jugar a la següent.

●Condicions d'ús
https://cubecut.ultimate-math.com/pdf/terms_of_service_exp.pdf

●Política de privadesa
https://cubecut.ultimate-math.com/privacy_policy.html

Novetats

細かい修正。