Adding unit fractions
10 k+
Aflaaie
Almal
info
Meer oor hierdie app
Die app stel 21 uitdagings voor wat u moet oorkom.
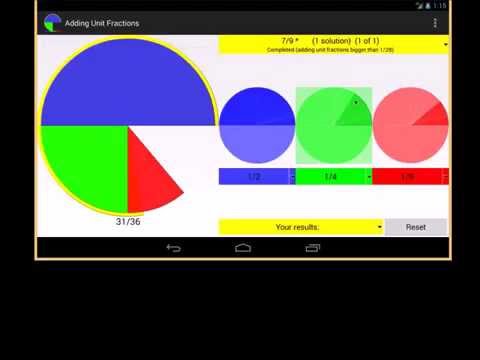
Verkry die regte breuke wat aan die bokant van die toepassing gelys is, en voeg twee of drie eenheidsbreuke by.
Elke voorgestelde regte breuk het 'n veranderlike aantal oplossings.
En verskillende vlakke van moeilikheidsgraad
U kan nie eenheidsbreuke met dieselfde waarde herhaal nie.
In die app vind u 'n knoppie om al die oplossings wat in die huidige probleem gevind word, uit te vee en van voor af te begin.
Die geringste eenheidsbreuk wat in hierdie app gebruik word, is 1/28.
Die program is ontwerp om die bruikbaarheid van die aftrekking van breuke in die oplossing van sulke probleme aan te toon.
Vanaf www.nummolt.com
Dit is 'n evolusie van die "Old Egyptian Fractions" wat in samewerking met www.mathcats.com gemaak is
wenk:
In die Rhind Mathematical Papyrus (RMP) in 1650 vC het die skrywer Ahmes die nou verlore toets vanaf die regering van die koning Amenemamhat III gekopieer.
Die eerste deel van die papyrus word deur die 2 / n-tabel opgeneem. Die breuke 2 / n vir onewe n wat wissel van 3 tot 101 word uitgedruk as somme van eenheidsbreuke.
In hierdie app kan u 'n paar van die Ahmes-ontbindings (2/3, 2/5, 2/7, 2/9) bou en die weggegooide deur hom ook.
Die app laat toe om ook te ontbind: 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10.
U kan die kennis wat u opgedoen het gebruik om die 2 / n-ontledings op te los om die res van die probleme op te los.
Meer: http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html
Die app "Behoorlike breuke" (dieselfde ontwikkelaar) is die regte hulpmiddel wat help om 'optel van eenheidsbreuke' op te los
Merlot verwysing van hierdie app:
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
kursusse:
Wiskunde 1, 2 en 3: breuke
Wiskunde 4: Skryf van breuke, ekwivalente breuke, Vergelyk en orden, breuke vereenvoudig, breuke optel, breuke aftrek
Wiskunde 5, 6 en 7: Skryf van breuke, ekwivalente breuke, Vergelyk en orden, breuke vereenvoudig, breuke optel, breuke aftrek, breuke vermenigvuldig, breuke deel
Van: nummolt.com
Nummolt-programme:
"Wiskunde is die moeilikste speelding. Hoe onheilspellend ookal 'n kind is, sal dit nooit kan breek nie."
Verkry die regte breuke wat aan die bokant van die toepassing gelys is, en voeg twee of drie eenheidsbreuke by.
Elke voorgestelde regte breuk het 'n veranderlike aantal oplossings.
En verskillende vlakke van moeilikheidsgraad
U kan nie eenheidsbreuke met dieselfde waarde herhaal nie.
In die app vind u 'n knoppie om al die oplossings wat in die huidige probleem gevind word, uit te vee en van voor af te begin.
Die geringste eenheidsbreuk wat in hierdie app gebruik word, is 1/28.
Die program is ontwerp om die bruikbaarheid van die aftrekking van breuke in die oplossing van sulke probleme aan te toon.
Vanaf www.nummolt.com
Dit is 'n evolusie van die "Old Egyptian Fractions" wat in samewerking met www.mathcats.com gemaak is
wenk:
In die Rhind Mathematical Papyrus (RMP) in 1650 vC het die skrywer Ahmes die nou verlore toets vanaf die regering van die koning Amenemamhat III gekopieer.
Die eerste deel van die papyrus word deur die 2 / n-tabel opgeneem. Die breuke 2 / n vir onewe n wat wissel van 3 tot 101 word uitgedruk as somme van eenheidsbreuke.
In hierdie app kan u 'n paar van die Ahmes-ontbindings (2/3, 2/5, 2/7, 2/9) bou en die weggegooide deur hom ook.
Die app laat toe om ook te ontbind: 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10.
U kan die kennis wat u opgedoen het gebruik om die 2 / n-ontledings op te los om die res van die probleme op te los.
Meer: http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html
Die app "Behoorlike breuke" (dieselfde ontwikkelaar) is die regte hulpmiddel wat help om 'optel van eenheidsbreuke' op te los
Merlot verwysing van hierdie app:
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
kursusse:
Wiskunde 1, 2 en 3: breuke
Wiskunde 4: Skryf van breuke, ekwivalente breuke, Vergelyk en orden, breuke vereenvoudig, breuke optel, breuke aftrek
Wiskunde 5, 6 en 7: Skryf van breuke, ekwivalente breuke, Vergelyk en orden, breuke vereenvoudig, breuke optel, breuke aftrek, breuke vermenigvuldig, breuke deel
Van: nummolt.com
Nummolt-programme:
"Wiskunde is die moeilikste speelding. Hoe onheilspellend ookal 'n kind is, sal dit nooit kan breek nie."
Opgedateer op
Veiligheid begin wanneer jy verstaan hoe ontwikkelaars jou data insamel en deel. Praktyke vir dataprivaatheid en -sekuriteit kan verskil op grond van jou gebruik, streek en ouderdom. Die ontwikkelaar het hierdie inligting verskaf en kan dit mettertyd opdateer.
Geen data word met derde partye gedeel nie
Kom meer te wete oor hoe ontwikkelaars datadeling verklaar
Geen data ingesamel nie
Kom meer te wete oor hoe ontwikkelaars insameling verklaar
Daartoe verbind om die Play Gesinsbeleid te volg
Wat's nuut
name 1.1.6 v.12 Update to Android 13 sdk34 + Privacy Policy
Appsteundienste
phone
Foonnommer
+34600336495
Meer oor die ontwikkelaar
Maurici Carbó Jordi
double.struck.capital@gmail.com
C. SAN ANTONI MARIA CLARET 324 46
08041 Barcelona
Spain
undefined