究極の立体＜切断＞

hanamarugroup

Acerca desta aplicación

● O primeiro dunha serie de preparacións definitivas para o exame de acceso á escola secundaria creada por un equipo de desenvolvedores de aplicacións educativas con 1 millón de usuarios.
● Analizouse 10 anos de preguntas pasadas de escolas famosas e seleccionou coidadosamente 100 preguntas.
● Domina o campo que aparece con frecuencia dos exames de acceso á escola secundaria, o ``corte tridimensional''!

◆Que tipo de material didáctico é o último tridimensional?

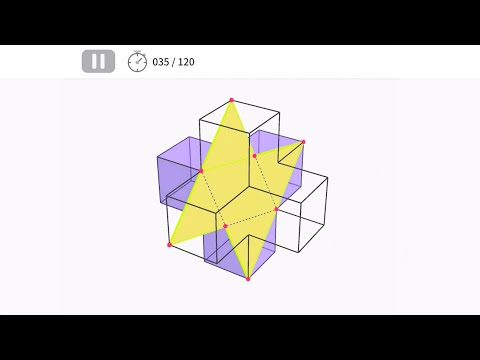
Esta é unha aplicación de material didáctico que contén 100 problemas sobre o ``corte 3D'', un campo que aparece con frecuencia nas matemáticas do exame de acceso ao bacharelato, e que permite rotar e cortar libremente os obxectos 3D reproducidos mentres aprendes.
Ao condensar os coñecementos sobre materiais didácticos de aplicación de Hanamaru Lab, que desenvolve a aplicación de desenvolvemento da capacidade de pensamento ``Think Think'' con 1 millón de usuarios, e os coñecementos sobre as guías de exames de acceso á escola secundaria da famosa escola cram ``Hanamaru Gakushukai'', desenvolvemos un método de corte tridimensional. Cultiva a capacidade de ``imaxinar como miras un problema''.
Este libro contén 100 preguntas que abarcan todos os patróns, baseadas nunha análise de preguntas tridimensionais reais de corte que se fixeron nos exames de matemáticas de acceso á escola secundaria nos últimos 10 anos.


◆Por que é importante o corte en 3D?
- Campos que aparecen con frecuencia nas probas de acceso ao bacharelato. O debuxo preciso en sección transversal é esencial!
O corte tridimensional é unha área importante e frecuente nas matemáticas para os exames de acceso á escola secundaria. As preguntas adoitan facerse como preguntas grandes e, se non podes debuxar o plano de corte con precisión, hai moitos casos nos que fallarás todas as preguntas. Ser capaz de imaxinar e debuxar con precisión un diagrama de sección transversal é un requisito previo importante para abordar un problema.

- É difícil aprender nunha pizarra ou en papel!
Díxose que o corte tridimensional é difícil de manexar porque require unha conciencia espacial avanzada e capacidade de manipulación de imaxes. Por moito que estudes nunha superficie plana como un encerado ou un papel, aínda que penses que o entendes nese momento, hai moitos casos nos que se cambia un pouco o ángulo ou cambia o punto de corte non o entenderás. en absoluto. Moitas familias intentaron cortar vexetais e esponxas na casa por proba e erro, pero este método era difícil de reproducir formas complexas e cortar superficies, e non era axeitado para a aprendizaxe repetida.

- Se o dominas, será unha gran vantaxe!
A pesar de ser un campo importante, moitos examinados loitan con el, pero se o dominas, terás unha enorme vantaxe. ``Ultimate 3D Cutting'' consegue os tres puntos seguintes: 1) mover e cortar o obxecto 3D vostede mesmo, 2) estudar coidadosamente as preguntas máis frecuentes do exame de acceso á escola secundaria e 3) estudar repetidamente os tres principios. Este é o único aplicación que che permite especializarte no corte en 3D utilizando un enfoque completamente diferente da aprendizaxe anterior.



◆Tres principios de corte tridimensional

1. "O mesmo plano": "Se hai dous puntos no mesmo plano, o corte pasará sempre pola recta que une os dous puntos. Polo tanto, pódense conectar puntos do mesmo plano.

2. "Paralelas": se as superficies son paralelas, as liñas de corte en cada superficie serán sempre paralelas. Polo tanto, se xa se trazou unha recta no plano B que é paralela ao plano A, podes trazar unha recta no plano A que pase polo punto e sexa paralela á recta no plano B.

3. "Estender": ao estender a liña de corte e os lados do sólido, podes atopar un punto fóra do sólido onde o corte pasa pola intersección. Podes trazar unha liña desde o punto atopado usando 1. ``coplanar'' e 2. ``paralelo''.


◆Obxecto deste material didáctico
As matemáticas do exame de acceso á escola secundaria xaponesa están cheas de preguntas interesantes e marabillosas que pon a proba as túas habilidades de pensamento e imaxinación.
Cremos que o acto de afrontar e resolver estes problemas debe ser unha experiencia intelectualmente emocionante e emocionante.
Por outra banda, é certo que debido ao alto nivel de habilidades de pensamento e imaxinación que se require, os resultados da aprendizaxe tradicional en papel ou encerados tendían a atribuírse ao ``sentido innato''.
Agardamos que as matemáticas para os exames de acceso á escola secundaria se convertan nunha experiencia de aprendizaxe intelectualmente dinámica na que todos poidan participar con entusiasmo. Comezaremos centrándonos no "corte tridimensional", que é unha materia que se atopa con frecuencia e que moitos os nenos teñen dificultades.Fíxeno un tema.
Como é unha aplicación, podes reproducir o obxecto 3D coma se o tiveses na man. A medida que te divirtes aprendendo mentres rotas e cortas sólidos perfectamente reproducidos, poderás visualizar calquera superficie de corte, reproducir, rotar e cortar o sólido da túa cabeza sen depender da técnica nin da memorización.
Cremos que ser capaz de converter un punto débil nun punto forte dará aos nenos unha sólida sensación de confianza, e que as habilidades de conciencia espacial que desenvolven se converterán nun gran activo, máis aló de estudar, mesmo despois de facer a proba de acceso.

◆Como usar
・Seleccione o problema que quere xogar na pantalla de selección de problemas.
- Premendo cada un dos tres botóns (3 principios de corte en 3D) na parte inferior dereita da pantalla de reprodución e tocando a superficie que desexa debuxar unha liña, só pode debuxar unha liña se a resposta é correcta.
- Unha vez debuxadas todas as liñas que compoñen o corte, mostraranse os resultados da xogada.
・Cada vez que remates de resolver unha pregunta, poderás xogar coa seguinte.

●Condicións de uso
https://cubecut.ultimate-math.com/pdf/terms_of_service_exp.pdf

●Política de privacidade
https://cubecut.ultimate-math.com/privacy_policy.html

Novidades

細かい修正。