究極の立体＜展開＞

Hanamarugroup

આ ઍપનું વર્ણન

● 1 મિલિયન વપરાશકર્તાઓ સાથે શૈક્ષણિક એપ્લિકેશન ડેવલપર્સની ટીમ દ્વારા નિર્ધારિત જુનિયર હાઇસ્કૂલ પ્રવેશ પરીક્ષા તૈયારી શ્રેણીની બીજી આવૃત્તિ!
● વિખ્યાત શાળાઓના ભૂતકાળના 10 વર્ષના પ્રશ્નોનું વિશ્લેષણ કર્યું અને 100 પ્રશ્નો કાળજીપૂર્વક પસંદ કર્યા!
● જુનિયર હાઈસ્કૂલની પ્રવેશ પરીક્ષાઓ, ``વિકાસ આકૃતિઓ''ના વારંવાર દેખાતા ક્ષેત્રમાં નિપુણતા મેળવો!

◆ અંતિમ ત્રિ-પરિમાણીય કેવા પ્રકારની શિક્ષણ સામગ્રી છે?

આ એક શિક્ષણ સામગ્રી એપ્લિકેશન છે જેમાં ``ડિપ્લોયમેન્ટ ડાયાગ્રામ' પરના 100 પ્રશ્નો છે, જે મિડલ સ્કૂલની પ્રવેશ પરીક્ષાઓ માટે ગણિતમાં વારંવાર બનતું ક્ષેત્ર છે, અને તમને એસેમ્બલ કરવામાં આવતા અને સમજવામાં સરળ ડેવલપમેન્ટ ડાયાગ્રામના એનિમેશન દ્વારા શીખવાની મંજૂરી આપે છે. સમજૂતીત્મક ચિત્રો.
અમે હનામારુ લેબની એપ્લિકેશન શીખવવાની સામગ્રી વિશેની માહિતીને સંક્ષિપ્ત કરી છે, જે 1 મિલિયન વપરાશકર્તાઓ સાથે વિચાર ક્ષમતા વિકાસ એપ્લિકેશન ``થિંક સિંક'' વિકસાવે છે અને પ્રખ્યાત ક્રેમ સ્કૂલની જુનિયર હાઇસ્કૂલ પ્રવેશ પરીક્ષા માર્ગદર્શનનું જ્ઞાન ધરાવે છે. હનામારુ ગાકુશુકાઈ''. ત્રિ-પરિમાણીય પદાર્થની કલ્પના કરવાની ભાવના કેળવો.
અમે છેલ્લાં 10 વર્ષોમાં જુનિયર હાઈસ્કૂલની પ્રવેશ પરીક્ષાના ગણિતમાં ખરેખર પૂછેલા વિકાસ ડાયાગ્રામ પ્રશ્નોનું વિશ્લેષણ કર્યું, અને પેટર્નને આવરી લેતા 100 પ્રશ્નોનો સમાવેશ કર્યો.


◆ "વિકાસ રેખાકૃતિ" શા માટે મહત્વપૂર્ણ છે?

- ક્ષેત્રો જ્યાં કોઈ સ્પષ્ટ ઉકેલ નથી. છબી શક્તિ એ વ્યૂહરચના માટેની ચાવી છે!
ત્રિ-પરિમાણીય વિકાસ આકૃતિઓ માટે કોઈ સ્પષ્ટ ઉકેલ નથી, અને કલ્પના શક્તિ મહત્વની છે. વાસ્તવિક જુનિયર હાઈસ્કૂલની પ્રવેશ પરીક્ષાઓમાં, પ્રશ્નો મોટાભાગે મોટા પ્રશ્નો (*) તરીકે પૂછવામાં આવે છે, અને જો તમે ત્રિ-પરિમાણીય છબીની કલ્પના કરી શકતા નથી, તો એવા ઘણા કિસ્સાઓ છે જ્યાં તમે બધા મોટા પ્રશ્નોમાં નિષ્ફળ જાઓ છો. આ ક્ષેત્રમાં, સફળતાની ચાવી એ છે કે તમે વિકસિત રેખાકૃતિમાંથી એસેમ્બલ થનારી ત્રિ-પરિમાણીય રચનાને કેટલી સરળ રીતે વિઝ્યુઅલાઈઝ કરી શકો છો.
(*) મિડલ સ્કૂલ પ્રવેશ પરીક્ષા ગણિતમાં મોટાભાગે 4-7 મોટા પ્રશ્નો હોય છે, અને દરેક મોટા પ્રશ્નમાં સામાન્ય રીતે 3-5 પેટા-પ્રશ્નો હોય છે.

- બ્લેકબોર્ડ અથવા કાગળમાંથી છબી મેળવવી મુશ્કેલ છે!
3D કટીંગની જેમ, તે પ્રાપ્ત કરવું મુશ્કેલ ક્ષેત્ર છે કારણ કે તેને અદ્યતન અવકાશી જાગૃતિ અને છબી મેનીપ્યુલેશન કુશળતાની જરૂર છે. બ્લેકબોર્ડ પર અથવા કાગળ પર, વિકાસ રેખાકૃતિમાંથી એસેમ્બલ કરવામાં આવશે તે ત્રિ-પરિમાણીય માળખાની કલ્પના કરવી અત્યંત મુશ્કેલ છે, અને આ ઘણા પરીક્ષણ લેનારાઓ માટે મુશ્કેલીનું કારણ છે. વિચાર મેળવવા માટે, શ્રેષ્ઠ તાલીમ એ ખરેખર તેને એસેમ્બલ કરવાની છે, પરંતુ જો તમે કાગળ પર એક રેખાકૃતિ દોરો અને પછી તેને દરેક વખતે એસેમ્બલ કરો, તો તે એકલા મોટા પ્રમાણમાં પ્રયત્નો અને સમય લેશે.

- વધુ સમય લીધા વિના ઉત્તમ પરિણામો!
એનિમેશન અને ચિત્રો દ્વારા, તમે ટૂંકા ગાળામાં ઇમેજ તાલીમનું પુનરાવર્તન કરી શકો છો, અને વિસ્તાર અને વોલ્યુમ ગણતરીના ખ્યાલને પણ માસ્ટર કરી શકો છો જે તમામ ત્રિ-પરિમાણીય સમસ્યાઓ માટે સામાન્ય છે. બિનજરૂરી રીતે પ્રશ્નોની સંખ્યામાં વધારો કરવાને બદલે, તે નિપુણતા માટે જરૂરી 100 પ્રશ્નો કાળજીપૂર્વક પસંદ કરે છે અને રેકોર્ડ કરે છે, તેથી તે એક એવી એપ્લિકેશન છે કે જે જુનિયર હાઈસ્કૂલની પ્રવેશ પરીક્ષાઓ પહેલાં જ ઉકેલી શકાય છે, તે પરીક્ષાર્થીઓ માટે શક્તિશાળી સહયોગી બનાવે છે. બીજા ભાગમાં, અમે પડકારરૂપ પ્રશ્નો તૈયાર કર્યા છે જે જુનિયર હાઈસ્કૂલની પ્રવેશ પરીક્ષાના સ્તરથી આગળ વધે છે, જેથી તમે તેમને હલ કરવામાં મજા લઈને અદ્યતન અવકાશી જાગૃતિ અને ઈમેજ મેનીપ્યુલેશન કૌશલ્ય પ્રાપ્ત કરી શકો.



◆ "છ મૂળભૂત આકારો" જે ઘન બનાવે છે

જટિલ ઘન પદાર્થોને પણ છ મૂળભૂત આકારો (ત્રિકોણાકાર પ્રિઝમ, ત્રિકોણાકાર પિરામિડ, ચોરસ પ્રિઝમ, ચોરસ પિરામિડ, સિલિન્ડર અને શંકુ) માં વિભાજીત કરીને સરળતાથી ઉકેલી શકાય છે.
આ પદ્ધતિ વિકસિત આકૃતિઓ સિવાયની 3D ભૂમિતિ સમસ્યાઓ પર પણ લાગુ કરી શકાય છે, તેથી આ એપ્લિકેશનનો ઉપયોગ 3D ભૂમિતિ ક્ષેત્રમાં ચતુર્થાંશ સમસ્યાઓ ઉકેલવા માટે પણ થઈ શકે છે.　　


◆ આ શિક્ષણ સામગ્રીનો હેતુ
અમારા પ્રતિનિધિ કાવાશિમાના જુનિયર હાઈસ્કૂલની પ્રવેશ પરીક્ષાઓ શીખવવાના અનુભવના આધારે, અમે 3D આકારના ક્ષેત્ર પર ધ્યાન કેન્દ્રિત કર્યું, જેનો વારંવાર ઉપયોગ થતો હોવા છતાં, બ્લેકબોર્ડ પર અથવા વન-ઓન-વનમાં શીખવવામાં આવે ત્યારે બાળકો માટે કલ્પના કરવી અને ગતિશીલ અનુભવવું મુશ્કેલ છે. એનાલોગ સૂચના.
"અલ્ટિમેટ 3D" શ્રેણીમાં, અમે 3D ઑબ્જેક્ટ્સને ફરીથી બનાવવા માટે એપ્લિકેશનની લાક્ષણિકતાઓનો લાભ લઈએ છીએ જાણે તમે તેને તમારા હાથમાં પકડી રાખતા હોય. પરિણામ સ્વરૂપે, તમે વિચારવાની આવશ્યક રીતો મેળવી શકો છો જે કાગળ પર મોટી સંખ્યામાં સમાન સમસ્યાઓ જેમ કે ડ્રીલ્સ અને સમસ્યા સેટ કરીને મેળવી શકાતી નથી. જેમ જેમ તમે આ એપ્લિકેશનમાં દરેક પ્રશ્નનો ઉકેલ લાવવાનો આનંદ માણો છો, તેમ તમે સ્વાભાવિક રીતે તમારી અવકાશી જાગૃતિનો વિકાસ કરશો.

◆ કેવી રીતે ઉપયોગ કરવો
・સમસ્યા પસંદગી સ્ક્રીનમાંથી તમે જે સમસ્યા ચલાવવા માંગો છો તે પસંદ કરો.
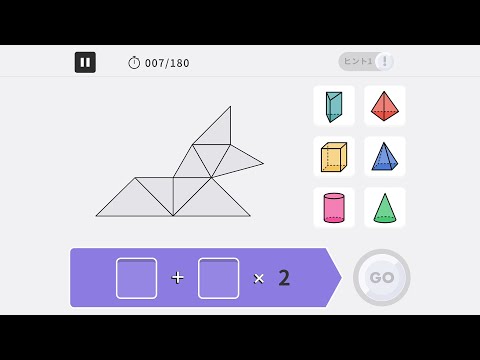
・પ્લે સ્ક્રીનની જમણી બાજુના 6 બટનો (6 મૂળભૂત આકારો)માંથી, સ્ક્રીનના તળિયે ચોરસને લાગુ પડે છે તે પસંદ કરો.
・જ્યારે બધા ચોરસ ભરાઈ જાય, ત્યારે GO બટન દબાવો.
・ જ્યારે પણ તમે એક પ્રશ્ન હલ કરવાનું સમાપ્ત કરો છો, ત્યારે તમે આગલો પ્રશ્ન રમી શકશો.

●ઉપયોગની શરતો
https://expansion.ultimate-math.com/pdf/terms_of_service_exp.pdf

●ગોપનીયતા નીતિ
https://expansion.ultimate-math.com/privacy_policy.html

નવું શું છે?

細かい修正