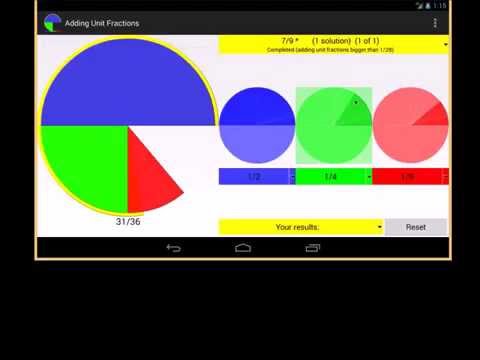
Adding unit fractions

nummolt

Հավելվածի մասին

Հավելվածն առաջարկում է հաղթահարել 21 մարտահրավեր:
Դիմումի վերին մասում նշված պատշաճ ֆրակցիաների ձեռքբերում, ավելացնելով երկու կամ երեք միավորի կոտորակներ:

Յուրաքանչյուր առաջարկվող համապատասխան մասն ունի լուծումների տարբեր փոփոխական շարք:
Եվ դժվարության տարբեր մակարդակներ

Դուք չեք կարող կրկնել նույն արժեքի միավորի կոտորակները:
Ծրագրում կգտնեք կոճակ `ջնջելու համար առկա խնդրի բոլոր լուծումները և զրոյից սկսել:
Այս հավելվածում օգտագործված ամենափոքր միավորի բաժինը 1/28 է:

Ծրագիրը կոչված է ցույց տալու խմբակցությունների հանման օգտակարությունը նման խնդիրների լուծման գործում:

Www.nummolt.com- ից
Սա է «Հին Եգիպտոսի Կոտորակները» էվոլյուցիան է, որոնք արվել են www.mathcats.com- ի հետ համագործակցությամբ

Հուշում
Մ.թ.ա. 1650 թ.-ին Ռինդի մաթեմատիկական պապիրուսում (RMP) դպիր Ահմեսը կրկնօրինակում էր այժմ կորցրած փորձությունը Amenemamhat III թագավորի տիրապետությունից:
Պապիրուսի առաջին մասը վերցված է 2 / n աղյուսակով: 3/101-ից սկսած տարօրինակ n-ի համար 2 / n ֆրակցիաները արտահայտվում են որպես միավորի ֆրակցիաների գումարներ:
Այս հավելվածում կարող եք կառուցել Ահմեսի որոշ տարրալուծումներից (2/3, 2/5, 2/7, 2/9) և նրա կողմից անտեսվածները:
Հավելվածը թույլ է տալիս քայքայվել նաև. 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10:
Մնացած խնդիրները լուծելու համար կարող եք օգտագործել 2 / n տարրալուծումները լուծելիս ձեռք բերված գիտելիքները:
Ավելին ՝ http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html

«Erիշտ ֆրակցիաներ» ծրագիրը (նույն մշակողը) ճիշտ գործիքն է, որն օգնում է լուծել «միավորի կոտորակները ավելացնելը»

Այս ծրագրի Merlot հղումը.
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
Դասընթացներ.
Մաթեմատիկա 1, 2 և 3: Կոտորակները
Մաթեմատիկա 4. Գրելու ֆրակցիաներ, համարժեք ֆրակցիաներ, համեմատություն և պատվիրում, ֆրակցիաների պարզեցում, ֆրակցիաների ավելացում, ֆրակցիաների հանում
Մաթեմատիկա 5, 6 և 7. Գրությունների խմբակցություններ, համարժեք ֆրակցիաներ, համեմատություն և կարգադրություն, ֆրակցիաների պարզեցում, ֆրակցիաների ավելացում, ֆրակցիաների իջեցում, բազմապատկիչ ֆրակցիաներ, բաժանում ֆրակցիաներ

Nummolt.com- ից
Nummolt ծրագրեր.
«Մաթեմատիկան ամենադժվար խաղն է: Այնուհանդերձ, չար երեխան կարող է լինել, երբեք չի կարողանա դրանք կոտրել»:

Ինչ նոր բան կա

name 1.1.6 v.12 Update to Android 13 sdk34 + Privacy Policy