Adding unit fractions

Name: Adding unit fractions
Availability: InStock
Author: nummolt

nummolt

10 миң+

жолу жүктөлүп алынды

Баары

Колдонмо тууралуу

Колдонмо 21 көйгөйдү чечүүнү сунуштайт.
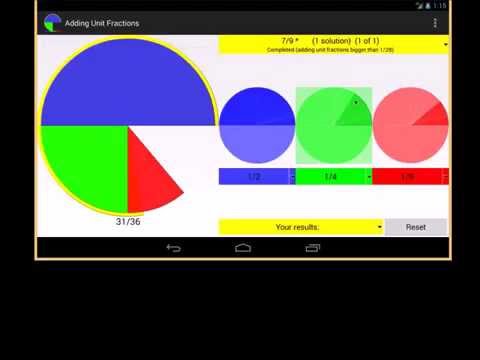
Колдонмонун үстү жагында көрсөтүлгөн тиешелүү фракцияларды алуу, эки же үч бирдиктүү фракцияларды кошуу.

Ар бир сунушталган туура бөлчөк өзгөрмөлүү сандагы чечимдерге ээ.
Жана ар кандай деңгээлдеги кыйынчылыктар

Бирдиктүү фракциялардын маанисин бирдей кайталай албайсыз.
Колдонмодо учурдагы көйгөйдү тапкан бардык чечимдерди жок кылып, нөлдөн баштап баскычты таба аласыз.
Бул колдонмодо колдонулган littlest бирдигинин үлүшү 1/28.

Программа мындай көйгөйлөрдү чечүүдө фракцияларды кыскартуунун пайдалуулугун көрсөтүү үчүн иштелип чыккан.

Www.nummolt.com сайтынан
Бул www.mathcats.com менен биргеликте жасалган "Эски Египеттин Фракцияларынын" эволюциясы

Hint:
Биздин заманга чейинки 1650-жылы Рейндеги Математикалык Папируста (RMP) катчы Ахмес Аменемамхат III падышанын тушунан жоголгон тестти көчүргөн.
Папирустун биринчи бөлүгү 2 / n таблицада орун алган. 3төн 101ге чейинки так n үчүн 2 / n фракциялар бирдиктүү фракциялардын суммасы катары көрсөтүлөт.
Бул колдонмодо сиз Ахметтин айрым бөлүктөрүн (2/3, 2/5, 2/7, 2/9) жана өзү таштап салган нерселерди түзө аласыз.
Колдонмо ошондой эле бөлүнүп чыгууга мүмкүнчүлүк берет: 3/4, 3/5, 4/5, 5/6, 3/7, 4/7, 5/7, 3/8, 5/8, 7/8, 4/9 , 5/9, 7/9, 8/9, 3/10, 7/10, 9/10.
Калган көйгөйлөрдү чечүү үчүн, 2 / n ажыроону чечүүдө алган билимиңизди колдонсоңуз болот.
Көбүрөөк: http://nummolt.blogspot.com/2014/12/adding-unit-fractions.html

"Таза фракциялар" тиркемеси (ошол эле иштеп чыгуучу) "бирдиктүү фракцияларды кошуу" маселесин чечүүгө жардам берет.

Бул колдонмонун Merlot маалымдамасы:
https://www.merlot.org/merlot/viewMaterial.htm?id=917779
сабактар:
Математика 1, 2 жана 3: Фракциялар
Математика 4: Жазуу фракциялары, Эквиваленттүү фракциялар, Салыштыруу жана иреттөө, Жөнөкөйлөштүрүлгөн фракциялар, Фракциялар кошуу, Бөлүп чыгаруу
Математика 5, 6 жана 7: Жазуу фракциялары, Эквиваленттүү фракциялар, Салыштыруу жана иреттөө, Жөнөкөйлөштүрүлгөн фракциялар, Фракциялар кошуу, Фракцияларды азайтуу, Көбөйтүүчү фракциялар, Бөлүүчү фракциялар

Кимден: nummolt.com
Nummolt колдонмолору:
"Математика - бул эң оор оюнчук. Бала канчалык жаман болсо дагы, аларды эч качан сындырбайт".

Качан жаңырды

2023-ж., 16-ноя.

Маалыматтардын коопсуздугу

Коопсуздук дегенде колдонмонун маалыматты кантип топтоп, аны үчүнчү тараптар менен кантип бөлүшө турганын түшүнүү керек. Маалыматтардын купуялыгы жана коопсуздугу колдонмоңуздун иштетилишине, жүргөн аймагыңызга жана курагыңызга жараша болот. Маалыматты иштеп чыгуучу берип, маал-маалы менен жаңырып турат.