Number Series Calculator - AI
Contains ads
4.3star
775 reviews
1L+
Downloads
Everyone
info
About this app
Learn independently to solve number patterns, arithmetic progressions, and geometric series used in IQ tests. With powerful AI features, the app helps you analyze patterns, generate sequences, and find missing numbers instantly using advanced reasoning. Practice and improve your skills with the Interactive Test! Perfect for students, teachers, and math enthusiasts!
🚀 Key Features:
✔ Calculating missing numbers and letters in sequences using AI reasoning.
✔ Creating number series tests automatically using AI.
✔ Solve Missing & Next Numbers – Identify the next or missing term in any sequence.
✔ Sequence Formulas & Patterns – Recognize arithmetic, geometric, Fibonacci, and prime number series.
✔ Graphical Representations – Visualize sequences with detailed charts.
✔ Sum Calculations – Compute sums of terms, including partial sums.
✔ Custom Math Expressions – Enter complex fractions like 1/2, 2/3, ?/4 for accurate results.
✔ Custom Formulas (JavaScript Syntax) – Create and evaluate your own sequence formulas.
✔ Letter Sequences Support – Customize alphabets to solve letter-based patterns.
✔ No Internet Needed – Solve problems anytime, anywhere.
You can download the paid version without ads.
Visit Number Series Calculator Next
📘 Test Categories Include:
• Arithmetic Progression
• Geometric Progression
• Alternating Series
• Square/Cube Number Series
• Prime Number Series
• Fibonacci Series
• Complex & Other Series
• IQ Test
You can choose to focus on one category or take a Mixed Test with questions from all types, offering a comprehensive and engaging brain workout.
Whether you're learning or mastering number sequences, the new test mode makes it fun, challenging, and educational!
🔍 Perfect for Test Preparation:
📌 Online assessment tests for jobs
📌 Employment aptitude tests
📌 Pre-employment screening
📌 Competitive exams requiring number series reasoning
✨ Real Examples from IQ Tests:
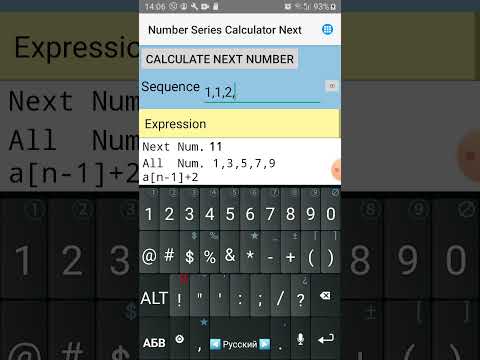
🔹 Fibonacci Sequence: 1, 1, 2, 3, 5, 8, 13 → Next Number = 21
🔹 Arithmetic Progression: 1, 3, 5, 7, 9, 11 → Next Number = 13
🔹 Geometric Progression: 1, 2, 4, 8, 16, 32 → Next Number = 64
👉 Download Number Series Calculator
🚀 Key Features:
✔ Calculating missing numbers and letters in sequences using AI reasoning.
✔ Creating number series tests automatically using AI.
✔ Solve Missing & Next Numbers – Identify the next or missing term in any sequence.
✔ Sequence Formulas & Patterns – Recognize arithmetic, geometric, Fibonacci, and prime number series.
✔ Graphical Representations – Visualize sequences with detailed charts.
✔ Sum Calculations – Compute sums of terms, including partial sums.
✔ Custom Math Expressions – Enter complex fractions like 1/2, 2/3, ?/4 for accurate results.
✔ Custom Formulas (JavaScript Syntax) – Create and evaluate your own sequence formulas.
✔ Letter Sequences Support – Customize alphabets to solve letter-based patterns.
✔ No Internet Needed – Solve problems anytime, anywhere.
You can download the paid version without ads.
Visit Number Series Calculator Next
📘 Test Categories Include:
• Arithmetic Progression
• Geometric Progression
• Alternating Series
• Square/Cube Number Series
• Prime Number Series
• Fibonacci Series
• Complex & Other Series
• IQ Test
You can choose to focus on one category or take a Mixed Test with questions from all types, offering a comprehensive and engaging brain workout.
Whether you're learning or mastering number sequences, the new test mode makes it fun, challenging, and educational!
🔍 Perfect for Test Preparation:
📌 Online assessment tests for jobs
📌 Employment aptitude tests
📌 Pre-employment screening
📌 Competitive exams requiring number series reasoning
✨ Real Examples from IQ Tests:
🔹 Fibonacci Sequence: 1, 1, 2, 3, 5, 8, 13 → Next Number = 21
🔹 Arithmetic Progression: 1, 3, 5, 7, 9, 11 → Next Number = 13
🔹 Geometric Progression: 1, 2, 4, 8, 16, 32 → Next Number = 64
👉 Download Number Series Calculator
Updated on
Safety starts with understanding how developers collect and share your data. Data privacy and security practices may vary based on your use, region, and age. The developer provided this information and may update it over time.
Ratings and reviews
4.2
756 reviews
Louis Ward
- Flag inappropriate
December 19, 2025
This math solver has been the number one " go to " for my every day encounters . It's like owning a virtual crystal ball .
PLATANUS
December 19, 2025
Thank you for the kind words!
April Hoi
- Flag inappropriate
December 7, 2020
You need to use , between numbers, I don't think a lot of people understand this. So maybe a little ? Icon that people can click to read how it works. Besides that it works perfectly, I like doing these riddles but if you get them wrong they don't always explain why. This app helps you figure out what they wanted.
16 people found this review helpful
PLATANUS
December 7, 2020
Thanks for the feedback and your ideas. In the next version of the
program, I will try to make the changes that you suggested.
A Delgado
- Flag inappropriate
August 30, 2023
Maybe it can be improvable, but it is an awesome idea. It can help in dramatic ways many activities. Thank you
4 people found this review helpful
PLATANUS
August 30, 2023
Thank you! If you have an idea how to improve the program, please write to me.
What’s new
New sequences added
App support
About the developer
BOAS GEORGIOS
platanussoft@gmail.com
ΚΑΛΛΙΘΕΑ
SKRA 19
KALLITHEA, ATTIKI 17673
Greece